السلام عليكم ،
هناك عمليات في الرياضيات ما نطلق عليه : من المناسب أن يكون كذلك
Adequate
مثل ب أس صفر = 1 و 0! = 1 ( 0! = 1 تعني مضروب الصفر Factorial )
بالنسبة لـ ب0 هي 1 ليس باستخدام التعريف و لكن لأننا نعلم
من طرق أخرى أنها 1 و لذلك نقول انها من المناسب أن تكون 1
لنرى ماذا يحصل عند إستخدام التعريف و سأستخدم لغة مبسطة :
ب2 = ب × ب : ب تظهر مرتين في عملية الضرب
ب3 = ب × ب × ب : ب تظهر 3 مرات في عملية الضرب
الآن من يستطيع تفسير
ب0 : ب تظهر صفر مرات في عملية الضرب
هل الجواب 1 : منطقيا و باستخدام التعريف هذا ليس ممكنا !!!!
و لكن لأننا نعلم علم اليقين بما يمكن إثباته رياضيا أن :
ب ÷ ب = 1
و أن ب ÷ ب = ب1 ÷ ب1 = ب 1 -1 = ب0
إذا من المناسب أن نقول ب0 = 1
و لكننا لا نستطيع ذلك باستخدام التعريف!
الآن بالنسبة لـ 0 ! ( مضروب الصفر )
ما هو مضروب العدد ن ، حيث ن عدد صحيح موجب؟
بالتعريف :
ن! = 1 × 2 × 3 × 4 × ......× ن
أمثلة:
5! = 1 × 2 × 3 × 4 × 5 = 120
1! = 1
4! = 1 × 2 × 3 × 4 = 24
إذا ما هو 0! باستخدام التعريف :
0! = 1 × 0 = 0 خطأ
لاننا لا نستطيع حسب التعريف العودة للصفر
نعود لكلمة مناسب ( Adequate ) ، بالرغم من أن هناك تبرير مقنع لذلك على
الشكل التالي :
نعلم من خلال التعريف القاعدة التالية :
مضروب العدد = مضروب العدد الذي يسبقه × العدد نفسه
ن! = (ن-1)! × ن
5! = (1×2×3×4 ) × 5
5! = 4! × 5
و عليه : 1! = 0! × 1
و منه 0! = 1
كيف يمكن أن نوّظف ذلك في التعريف ؟
علينا إعادة كتابة التعريف على الشكل التالي:
0! = 1
ن! = (ن-1)! × ن ، ن > صفر
ملحق :
ما أهمية 0! ؟
أحد أهم العمليات التي تحتاج 0! هي التوافيق ( Combinations )
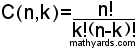
) هي عدد اختيارات k عناصر ماخوذة من مجموعة تحوي ن
هي عدد اختيارات k عناصر ماخوذة من مجموعة تحوي ن
عنصرا
ما هو عدد اختيارات 0 عنصرا من مجموعة تحوي ن عناصر ؟
ما هو عدد اختيارات ن عنصرا من مجموعة تحوي ن عناصر ؟
الجواب في الحالتين بدون استخدام القاعدة أعلاه = 1
و هذا الجواب مناسب و متوافق مع النتيجة التي
نحصل عليها فيما لو استخدمنا القاعدة :
ما هو عدد اختيارات 0 عنصرا من مجموعة تحوي ن عناصر ؟
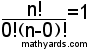
ما هو عدد اختيارات ن عنصرا من مجموعة تحوي ن عناصر ؟
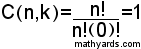
إذا 0! = 1 تتناسب مع ما توقعناه من إجابة السؤالين أعلاه





 آخر 10 مشاركات
آخر 10 مشاركات









