| اقتباس :
المشاركة الأصلية كتبت بواسطة أبو علي
[ مشاهدة المشاركة ]
|
بسم الله الرحمن الرحيم
العمل : نرسم الزاوية ك د جـ مساويةً للزاوية د ب هـ
والزاوية ل هـ ب مساويةً للزاوية هـ جـ د
كما في الشكل الأول
الإثبات ( من شقين ):
الشق الأول :
زاوية ن ب جـ = زاوية و د ن ( من العمل )
زاوية ن جـ ب = زاوية ل هـ ن ( من العمل )
زاوية ب ن جـ = زاوية د ن هـ ( بالتقابل بالرأس )
ولكن نعلم أن ن ب جـ + زاوية ن جـ ب + زاوية ب ن جـ = 180درجة لأنها زوايا داخلية في المثلث
إذاً زاوية و د ن + زاوية ل هـ ن + زاوية د ن هـ = 180 درجة
بما أن مجموع زوايا الرباعي = 360 درجة
إذاً زاوية د و هـ = 360 – ( زاوية و د ن + زاوية ل هـ ن + زاوية د ن هـ ) = 180درجة
أي أنها زاوية مستقيمة
وعليه فإن ( النقطة د ) و( النقطة و ) و( النقطة هـ ) على استقامة واحدة
إذاً سيكون د هـ ب مثلث وكذلك د هـ جـ سيكون مثلث
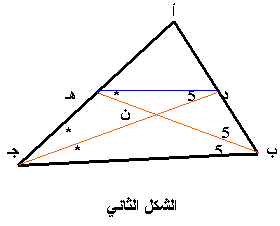
واستناداً على هذا الاستنتاج سنثبت الشق الثاني من البرهان ( إن شاء الله ) من خلال الشكل الثاني
الشق الثاني من البرهان :
المثلث د هـ ب يطابق المثلث هـ جـ د
لأن زاوية هـ د جـ = زاوية د ب هـ
وزاوية هـ جـ د = زاوية د هـ ب
وطول ب هـ = طول د جـ ( معطى )
إذاً ينطبق المثلثان وينتج تطابق عناصره الستة مثنى مثنى ( ثلاثة زوايا وثلاثة أضلاع )
وبما أن زاوية هـ جـ د = زاوية د هـ ب
إذاً الضلعين المواجهين لهما يكونان متطابقان
إذاً طول د هـ = طول د ب
إذاً المثلث د ب هـ متطابق الضلعين
ونستنتج أن زاوية د ب هـ = زاوية د هـ ب
ولكن زاوية د ب هـ = نصف الزاوية أ ب جـ
وكذلك زاوية د هـ ب = نصف الزاوية أ جـ ب
إذاً الزاوية أب جـ = الزاوية أ جـ ب
وعليه يكون المثلث أ ب جـ متطابق الضلعين
وعفواً على الإطالة
أبو علي
|
أخى لايوجد حرف (و) فى الشكل
20-05-2008, 11:15 PM
العرض الشجري