المعادلات الديفونتية Diophantine Equations

18-06-2009, 12:16 AM

السلام عليكم و رحمة الله وبركاته

..

سأتحدث في هذا الموضوع عن المعادلات الديفونتية الخطية و عن نظم التكافئات الخطية ، و للعلم فأنا طالب و لذا كثيرا ما أخطأ فأرجو أن تصححوا لي

وقد قررت كتابة هذا الموضوع ليستفيد منه كل من يحب الرياضيات وهو بناء على تجربتي الشخصية ..

سأبدأ بتوضيح نقطة هامة جدا :

المعادلات الديفونتية الخطية هي معادلات من الدرجة الأولى نبحث لها عن حلول تنتمي إلى مجموعة الأعداد الصحيحة

فمثلا

هي معادلة ديوفنتية خطية في متغيرين.
و ليتمكن الجميع من فهم الرموز المستعملة سأعرف أكثرها شيوعا وسأبين معنى البقية عند الحاجة ..

الرموز الأساسية هي :
1. رمز قابلية القسمة

ويعني a تقسم b
2. رمز العامل المشترك الأكبر

و يعني العامل المشترك الأكبر للعددين a و b

الصورة العامة للمعادلة الديفونتية الخطية في متغيرين هي :

حيث كل الأعداد السابقة صحيحة..

و لتكون هذه المعادلات قابلة للحل لا بد أن يتحقق الشرط التالي :

فلنقل الآن أن لدينا معادلة ديفونتية خطية و لها حلول ،، يبقى السؤال الأهم: كيف نوجد هذه الحلول و كم هو عددها؟؟

و لنجيب عن هذا السؤال يجب أن نتعرف إلى مفهوم قد يكون جديدا على البعض ، وهو الحساب المقاسي modular arithmetic

يعتمد الحساب المقاسي على فكرة أن أي عدد يمكن كتابته بدلالة أي عدد آخر و ذلك على الصورة

حيث m و n أي عددين صحيحين، و q هو ناتج القسمة و r هو الباقي

و بذلك يمكننا أن " نكافئ" أي عددين صحيحن في " mod "عدد ما ، إذا تركا الباقي نفسه عند قسمة كل منهما عليه ،
فلنقل أن العدد a يترك الباقي نفسه الذي يتركه العدد b عند قسمتهما على العدد n حينها يمكننا أن نقول بصيغة رياضية :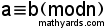

و لعلاقة التكافؤ هذه خواص جميلة سأشرحها في مشاركتي التالية ، و بعدما نتعرف على تلك الخواص سنكمل رحلتنا للبحث عن حلول المعادلات الديوفونتية..

أسأل الله التوفيق و عسى أن يستفيد أحد مما أكتب..

ملاحظة: لا تترددوا في السؤال عن أي شيء وسأحاول المساعدة على قدر استطاعتي

.


العضو المميز	الموضوع المميز	المشرف المميز
المنتدى متاح للتصفح فقط ولا يقبل المشاركات الجديدة	ماشاء الله تبارك الله ماشاء الله لاقوة الا بالله	المنتدى متاح للتصفح فقط ولا يقبل المشاركات الجديدة