

 |
 |

|
||
| العضو المميز | الموضوع المميز | المشرف المميز |
| المنتدى متاح للتصفح فقط ولا يقبل المشاركات الجديدة | ماشاء الله تبارك الله ماشاء الله لاقوة الا بالله | المنتدى متاح للتصفح فقط ولا يقبل المشاركات الجديدة |
 آخر 10 مشاركات
آخر 10 مشاركات
|
|
|||||||
| قوانين المنتديات | كيفية تحميل الملفات | سلسلة كيف | مدرج الرموز | تفعيل العضوية | استرجاع كلمة المرور | ابحث في المنتدى من جوجل |
 |
 |
 |
|
 |
 |
 |
|
|
رقم المشاركة : 1 | |
|
من مواضيعه : 0 أثبت أن 133 يقسم 11^(ن+2) + 12 ^ (2ن + 1) 0 س1:أثبت التعامد،س2:أوجد مساحةالمنطقةالمثلثية 0 مسألتان أرجو حلهما
شكراً: 0
تم شكره 0 مرة في 0 مشاركة
|
السؤال الاول
|
|
|
|
رقم المشاركة : 2 | |||||
|
من مواضيعه : 0 متوسطان متعامدان أوجد طول Ab من الشكل. 0 متباينة في المثلث (4) 0 حلل إلى عوامل (1) 0 مجموع مثلثي (3) 0 نهايات(ثانوي)
شكراً: 0
تم شكره 35 مرة في 27 مشاركة
|
http://www.uaemath.com/ar/aforum/showthread.php?t=4221
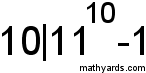 :Is this qustion such :Is this qustion such
|
|||||
|
|
رقم المشاركة : 3 | |
|
من مواضيعه : 0 مسألتان أرجو حلهما 0 أثبت أن 133 يقسم 11^(ن+2) + 12 ^ (2ن + 1) 0 س1:أثبت التعامد،س2:أوجد مساحةالمنطقةالمثلثية
شكراً: 0
تم شكره 0 مرة في 0 مشاركة
|
السؤال الاول
|
|
 |
|
|
 |
 |  |