

 |
 |

|
||
| العضو المميز | الموضوع المميز | المشرف المميز |
| المنتدى متاح للتصفح فقط ولا يقبل المشاركات الجديدة | ماشاء الله تبارك الله ماشاء الله لاقوة الا بالله | المنتدى متاح للتصفح فقط ولا يقبل المشاركات الجديدة |
 آخر 10 مشاركات
آخر 10 مشاركات
|
|
|||||||
| قوانين المنتديات | كيفية تحميل الملفات | سلسلة كيف | مدرج الرموز | تفعيل العضوية | استرجاع كلمة المرور | ابحث في المنتدى من جوجل |
 |
 |
 |
|
 |
 |
 |
|
|
رقم المشاركة : 1 | |||
|
من مواضيعه : 0 مثلثات هيرون 0 أكشن سكريبت للمساعدة فى عمل درس 0 رياضيات الصف الخامس والسادس (باور بوينت) 0 مواقع أعجبتني 0 مذكرة بالوورد - الأول الإعدادى - فصل أول
شكراً: 1,034
تم شكره 727 مرة في 375 مشاركة
|
إذا كان لدينا مثلث أطوال أضلاعه :أ ، ب ، جـ ...قتكون مساحته مساوية : للجذر التربيعى لحواصل ضرب (ح) (ح -أ ) ( ح - ب) (ح - جـ) حيث ح : نصف محيط المثلث = نصف مجموع أطوال أضلاعه. تحياتى للجميع.
|
|||
|
|
رقم المشاركة : 2 | |||||||
|
من مواضيعه : 0 قوانين المثلث العام 0 مسابقة أجمل حل : س4 0 نتيجة المسابقة الأولى 0 معادلة أسية 0 صندوق محرر اللاتيك
شكراً: 1,441
تم شكره 752 مرة في 288 مشاركة
|
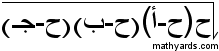
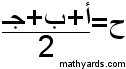  أمل على الموضوع الخفيف المفيد أمل على الموضوع الخفيف المفيد
|
|||||||
|
|
رقم المشاركة : 3 | |
|
من مواضيعه : 0 درس المتباينات:كتاب الكتروني + فلاشات متنوعة 0 للأطفال : قابلية القسمة على 5،2 - صوت وصورة 0 اقتراح : إنشاء قسم لتمارين هندسة موقع gogeometry 0 قوانين المثلث العام 0 أوراق عمل"العاشر"(الفصل الثاني2008)-الإمارات
شكراً: 1,034
تم شكره 727 مرة في 375 مشاركة
|
ولك كل الشكر التقدير لمرورك الرائع أستاذى الكريم
|
|
|
|
رقم المشاركة : 4 | |
|
من مواضيعه : 0 اثبت ان... 0 تعدييل(أثبت ان) 0 مثلثية فيها فكرة 0 تحذير من ......... 0 حاصل ضرب وتر وضلع = (س^4-1) /4 ، فما طولهما؟
شكراً: 1
تم شكره 26 مرة في 18 مشاركة
|
أثبت أن:
|
|
|
|
رقم المشاركة : 5 | |
|
من مواضيعه : 0 أدخل واكتب قانون رياضي 0 مسألة حلوة 0 مسائل معقد ة للمشاركة والنقاش 0 ثلاث معادلات 0 تحدي لشطار الجبر
شكراً: 1
تم شكره 26 مرة في 18 مشاركة
|
بما انكم تكتفون بالمشاهدة فقط سأعرض الحل:
|
|
|
|
رقم المشاركة : 6 | |||
|
من مواضيعه : 0 ضمير العرب ........صباح الخير,خاطرة 0 عن جد روعه ,,, 0 لغز جميل 0 أحتاجكم هنا ........حقا .. 0 علمي ول ادبي ....ادخل وشوف ,,,
شكراً: 0
تم شكره 4 مرة في 3 مشاركة
|
الحل حلو كتيير انا كتير حاولت وما عرفت أحله
|
|||
|
|
رقم المشاركة : 7 | |
|
شكراً: 0
تم شكره 0 مرة في 0 مشاركة
|
الف شكر اخي العزيز
|
|
|
|
رقم المشاركة : 8 | |
|
شكراً: 0
تم شكره 0 مرة في 0 مشاركة
|
|
|
|
|
رقم المشاركة : 9 | |||
|
شكراً: 0
تم شكره 0 مرة في 0 مشاركة
|
شكراااااااااااااااااااااا ااااااااااااااا
|
|||
|
|
رقم المشاركة : 10 | |
|
من مواضيعه : 0 تمارين هندسة من موقع gogeometry ( مع الحل) 0 تكامل جميل 0 مسائل لم تحل ( أرجو التعاون) 0 مستطيلات 0 الثابت k
شكراً: 460
تم شكره 465 مرة في 315 مشاركة
|
شكرا على البرهان
|
|
 |
|
|
 |
 |  |